Урок 8.2 - Двоичная логика

8.2. Логические уровни и двоичная система счисления

В предыдущем уроке мы познакомились с цифровыми сигналами. Теперь мы знаем, как можно преобразовать привычный нам аналоговый сигнал в цифровой в виде последовательности чисел.
Но вот незадача: оказывается, «капризные» цифровые схемы предпочитают работать не с любыми числами, а только с определёнными цифрами. Им подавай либо «0», либо «1». Но ведь в мире огромное множество разных чисел! И как же нам быть, как описать их все только двумя цифрами? Давайте разбираться.
Начнём с определения понятия «логический уровень».
Цифровые схемы понимают только два состояния: «нет сигнала» или «есть сигнал». Другими словами, состояние «нет сигнала» - это низкий логический уровень, или логический «0», состояние «есть сигнал» - высокий логический уровень, или логическая «1». Условились считать, что в электронике логической единице соответствует сигнал высокого напряжения, а логическому нулю – сигнал низкого напряжения.
На графике (рис.1.) это можно представить так:

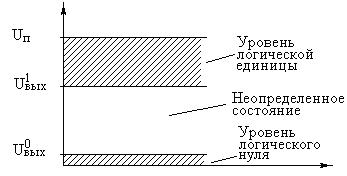
Рис.1. Высокий и низкий логический уровни

Обозначения на рисунке: Uп – это уровень напряжения питания; U1вых - уровень логической единицы, U0вых – уровень логического нуля.
Мы видим, что сигнал логической «1» может иметь напряжение не строго равное напряжению питания (Uп) или 0В, а находящееся в некотором диапазоне, ширина которого (Uп- U1вых). Так условились специально по причине того, что КПД микросхем не может быть 100% (из-за потерь на рассеивание тепла напряжение на выходе микросхемы всегда ниже её напряжения питания).
Эти же рассуждения справедливы и для уровня логического «0», который принимается равным чуть выше 0 Вольт.
Для разных микросхем ширина интервала логических «1» и «0» разная, поэтому на этом графике намеренно не указаны конкретные цифровые значения напряжений: для первого знакомства с цифровой схемотехникой этого не требуется.
А теперь поговорим о том, как преобразовывать любые числа в двоичный код, то есть в последовательность «нулей» и «единичек».
Есть простое правило перевода: для того, чтобы преобразовать десятичное число в двоичное, его нужно разложить по степеням двойки.
Возьмём, например, десятичное число 9 и разложим его по степеням двойки:
9: 24+23+22+21+20

Следующая наша задача – умножить каждое слагаемое правой части уравнения на 0 или 1, добившись равенства:
9 = 0х24+1х23+0х22+0х21+1х20

Последовательность нулей и единиц в правой части уравнения – это и есть двоичный код нашей девятки. Таким образом: 910 = 010012
Можете потренироваться сами, а для проверки приведём таблицу соответствия десятичных и двоичных числе от нуля до десяти (рис.2.):

Рис.2. Таблица соответствия десятичных чисел и двоичного кода

Таким же образом можно перевести любое десятичное число в двоичный вид. Например, число 245 в двоичной системе будет записано так: 11110101.
Процесс перевода чисел из одной системы в другую – это рутинная механическая работа, поэтому разумнее воспользоваться благами прогресса и поручить эту работу машинам. Есть специальные он-лайн программы и приложения для смартфонов, мгновенно переводящие числа из одной системы счисления в другую.
Конечно, мы рассмотрели двоичную систему счисления только в самом общем виде, но мы же начинающие электронщики, и для первого понимания основ этой информации достаточно. А в следующих уроках мы продолжим погружение в увлекательный мир цифровой схемотехники и поговорим о простейших логических элементах.